机器学习中的过拟合与欠拟合
在机器学习算法中,经常会遇到两个问题:欠拟合(underfitting)和过拟合(overfitting)。所谓欠拟合就是算法没有学习到足够的特征,预测结果较差,即拟合程度不够;过拟合则刚好相反,算法除了学习到一般特征外,也学习到了样本个体的局部特征,即拟合过度。
造成这两种结果的原因主要有两个:
(1)模型选择不好,简单问题选择了复杂的模型,容易过拟合;复杂的问题选择了简单的模型容易欠拟合。
(2)参数设置和调整有问题。特别存在学习率的方法,学习率调整不当,容易引起这两种结果。
1、白天鹅与黑天鹅问题
过拟合的一个形象的例子是白天鹅与黑天鹅例子。给一群天鹅让机器来学习天鹅的特征,经过训练后,算法学习到了以下特征:
(1)天鹅有翅膀,天鹅的嘴巴是长长的弯曲的,天鹅的脖子是长长的有点曲度,天鹅的整个体型像一个“2”且略大于鸭子。
这时,算法已经基本能区别天鹅和其他动物了。很不巧,训练样本中天鹅的羽毛全是白色的,这时:
(2)算法经过学习后,会认为天鹅的羽毛都是白的。当预测对象是黑色羽毛的黑天鹅时,算法会认为预测对象不是天鹅。
上面这个例子中,(1)中的规律都是对的,是所有天鹅都具备特征,也就是所谓的全局特征;(2)中的规律:天鹅的羽毛是白色的。这实际上只是样本的个体特征,并非所有天鹅的特征,也就是局部特征。如果算法只学习到了部分全局特征(即欠拟合),或者在学习到全局特征的同时,又学习到了局部特征(即过拟合),会导致无法识别黑天鹅的情况。
2、过拟合与欠拟合的产生原因
利用机器学习对训练集样本进行训练、学习样本数据的特征时,算法除学习到样本数据一般的、共性的特征外,也会学到仅训练样本特有的个体特征(视为噪声)。通常,前者称为全局特征,后者称为局部特征。
机器学习算法在学习过程中,无法区别局部特征和全局特征。在训练完成后,算法除学到全局特征外,也可能会学到一些训练样本的局部特征。由于新样本未含有训练样本所特有的局部特征,因此,算法学到的局部特征占比越高,对新样本预测正确的概率越低,即所谓的“泛化性”(或“鲁棒性”)变差,这是过拟合造成的最大问题。
过拟合是算法学习的太彻底,把训练样本的所有特征几乎都学到了。过多的局部特征(由于噪声带来的假特征),造成模型的“泛化性”和识别正确率较低。
一般,解决过拟合问题,从两方面入手:首先是训练样本,要具有代表性,局部特征尽量少。另一方面,算法在训练时,不能学习的太过彻底,降低学到局部特征和错误特征的几率,使得识别正确率得到优化。
3、解决过拟合的方法
解决过拟合的常见方法有:early stopping、数据集扩增(Data augmentation)、正则化(Regularization)、Dropout等。
3.1 Early Stopping
算法训练的过程,本质上是对算法参数进行迭代更新的过程,如梯度下降(Gradient descent)算法。Early stopping通过在算法对数据集训练收敛前停止迭代,来防止过拟合。具体方法是,在每一个Epoch结束时(1个Epoch是对所有训练数据遍历一轮)计算validation data的accuracy,当accuracy不再提高时,就停止训练。
Early Stopping方法很符合直观感受,因为accurary都不再提高了,继续训练也是无益的,只会拉长训练时间。该方法的一个重点是,怎样才认为accurary不再提高了呢?并不是说accuracy一降下来便认为不再提高了,因为可能经过这个Epoch后,accuracy降低了,但是随后的Epoch又让accuracy又上去了,所以不能根据一两次的连续降低就判断不再提高。一般的做法是,在训练的过程中,记录到目前为止最好的accuracy,当连续10次Epoch(或者更多次)没达到最佳accuracy时,则可以认为accuracy不再提高了。此时便可以停止迭代了(Early Stopping)。这种策略也称为“No-improvement-in-N”,N即Epoch的次数,可以根据实际情况取,如10、20、30……
3.2 数据集扩增
数据集扩增即需要得到更多的符合要求的数据,即和已有的数据是独立同分布的,或者近似独立同分布的。一般有以下方法:
- 从数据源头采集更多数据
- 复制原有数据并加上随机噪声
- 重采样
- 根据当前数据集估计数据分布参数,使用该分布产生更多数据等
3.3 正则化
正则化方法是指在进行目标函数或代价函数优化时,在目标函数或代价函数后面加上一个正则化项,一般有L1正则化与L2正则化等。
- L0正则化的值是模型参数中非零参数的个数。
- L1正则化表示各个参数绝对值之和。
- L2正则化标识各个参数的平方的和的开方值。
正则化会导致参数稀疏,一个好处是可以简化模型,避免过拟合。因为一个模型中真正重要的参数可能并不多,如果模型中所有参数都起作用,那么会过于偏重训练数据本身特征(局部特征),从而导致模型的范化能力较差。另一个好处是参数变少可以使整个模型获得更好的可解释性。且参数越小,模型就会越简单,这是因为越复杂的模型,越是会尝试对所有的样本进行拟合,甚至包括一些异常样本点(噪声),很容易造成在较小的区间里预测值产生较大的波动,这种较大的波动也反映了在这个区间里的导数很大,而只有较大的参数值才能产生较大的导数。因此复杂的模型,其参数值会比较大。
L1正则化趋向于使模型中起作用的参数减少(权值为0),而L2正则化则趋向于使得模型中各个参数的权值较小,甚至趋于0(但不会为0)。权值越小则对应特征对模型的影响就较小。这相当于对这部分无关特征做了一个惩罚,即使它们的值波动比较大,受限于参数值很小,也不会对模型的输出结果造成太大影响,也就使得模型不会习得这部分特征而发生过拟合。
简单的总结:L1正则化会趋向于产生少量的特征,而其他的特征都是0,可用于特征选择;L2正则化会选择更多的特征,但这些特征的权值都会接近于0。
3.3.1 L0正则化
由于稀疏的参数可以防止过拟合,因此用L0范数(非零参数的个数)来做正则化项是可以防止过拟合的。
直观上看,利用非零参数的个数,可以很好的来选择特征,实现特征稀疏的效果,具体操作时选择参数非零的特征即可。但因为L0正则化很难求解,是个NP难问题,因此一般采用L1正则化。L1正则化是L0正则化的最优凸近似,比L0容易求解,并且也可以实现稀疏的效果。
3.3.2 L1正则化
L1正则化在实际中往往替代L0正则化,来防止过拟合,也称为Lasso。
L1正则化之所以可以防止过拟合,是因为L1范数就是各个参数的绝对值相加得到的,而参数值大小和模型复杂度是成正比的。因此复杂的模型,其L1范数就大,最终导致损失函数就大,说明这个模型就不够好。
通常,L1正则化在目标函数后面加上参数的L1范数和项,即参数绝对值和与参数的积项,即:
\[ \begin{equation} C=C_0+\frac{\lambda}{n} \sum_w |w| \end{equation} \] 其中\(C_0\)代表原始的代价函数,\(n\)是样本数,\(\lambda\)是正则化项系数,衡量正则化项与\(C_0\)项的比重。最后一项即为L1正则项。使用L1正则化后,计算梯度时,\(w\)和\(b\)的梯度变为:
\[ \begin{equation} \frac{\partial C}{\partial w}=\frac{\partial C_0}{\partial w}+\frac{\lambda}{n} sgn(w) \label {weight-gradient} \end{equation} \]
\[\begin {equation} \frac{\partial C}{\partial b} = \frac{\partial C_0}{\partial b} \label {bias-gradient} \end {equation} \]
其中,\(sgn\)是符号函数,即\(w\)是正数时\(sng(w)\)为\(+1\),而\(w\)为负数时\(sng(w)\)为\(-1\)。注意式(\(\ref {bias-gradient}\))中,正则化项对bias项无贡献。参数更新使用下式:
\[\begin{equation} w := w + \alpha \frac{\partial C_0}{\partial w} + \beta \frac{\lambda}{n} sgn(w) \label{L1_weight_update} \end{equation}\] \[ \begin {equation} b: = b + \alpha \frac{\partial C_0}{\partial b} \label {L1-bias-update} \end {equation}\]
其中,梯度下降算法中,\(\alpha < 0\),\(\beta < 0\),而在梯度上升算法中则相反。
与式(\(\ref {L1_weight_update}\))做个比较,未经正则化的线性回归中,权值项\(w\)的更新方程为:
\[\begin{equation} w := w + \alpha \frac{\partial C_0}{\partial w} \label{normal_weight_update} \end{equation}\]
注意,未正则化的线性回归中,权值参数\(w\)的更新(式(\(\ref {normal_weight_update}\))),没有式(\(\ref {L1_weight_update}\))等号右侧第二项(即正则化项);包含了L1正则化项的线性回归称为\(Lasso\)回归。常数项\(b\)的更新方程同式\((\ref {L1-bias-update})\)。
可以看出,当\(w\)为正时,更新后\(w\)会变小;当\(w\)为负时,更新后\(w\)会变大;因此L1正则化项令那些原先处于\(0\)(即\(|w|≈0\))附近的参数\(w\)往\(0\)移动,使得部分参数为\(0\),从而降低模型的复杂度(模型的复杂度由参数决定),从而防止过拟合,提高模型的泛化能力。
L1正则化有个问题:L1范数在\(0\)处不可导,即\(|w|\)在\(0\)处不可导,因此在\(w\)为0时,使用原来的未经正则化的更新方程来对\(w\)进行更新,即令\(sgn(0)=0\),即:
\[ \begin{equation} sgn(w) = \left \{ \begin{matrix} 1 & (w>0)\\ 0 & (w=0)\\ -1 & (w<0) \end{matrix} \right. \end{equation} \]
3.3.2 L2正则化
L2正则化就是在代价函数后面再加上一个基于L2范数的正则化项,即: \[\begin{equation}C=C_0+\frac{\lambda}{2n}\sum_w w^2 \label{L2-regulation-1}\end{equation}\] 式(\(\ref {L2-regulation-1}\))中,等号右侧第一项\(C_0\)为原始的代价函数,第一项是L2正则化项,它是这样来的:所有参数\(w\)的平方的和,除以训练集的样本大小\(n\)。\(\lambda\)是正则化项系数,衡量正则化项与\(C_0\)项的比重。正则化项中的系数\(\frac {1}{2}\),主要是为了计算方便,正则化项求导时会产生一个\(2\),与\(\frac {1}{2}\)相乘刚好凑整。
使用L2正则化后,梯度的计算与L1正则化类似,\(w\)的梯度变为:
\[ \begin{equation} \frac{\partial C}{\partial w}=\frac{\partial C_0}{\partial w}+\frac{\lambda}{n} w \label {weight-gradient-2} \end{equation} \]
参数\(b\)的梯度表达式与式(\(\ref {bias-gradient}\))相同,且正则化项对bias项同样无贡献。
L2正则化使用下式对权值参数\(w\)进行更新: \[ \begin{equation} w := w + \alpha \frac {\partial \theta}{\partial w} + \beta \frac{\lambda}{n}w \label{L2-weight-update} \end{equation}\] 其中,梯度下降算法中,\(\alpha < 0\),\(\beta < 0\),而在梯度上升算法中则相反。
仍然以线性回归为例,将式(\(\ref {L2-weight-update}\))与式(\(\ref {normal_weight_update}\))做个比较,类似L1正则化,未正则化的线性回归不包含式(\(\ref {L2-weight-update}\))等号右侧第二项(L2正则化项)。包含L2正则化项的线性回归称为岭回归(\(Ridge \ Regression\))或权值衰减(\(weight \ decay\))。
与L1正则化类似,L2正则化项倾向于减小权值参数\(w\)(但不为0)。
顺便提一下参数的更新,在对模型参数进行学习更新时,常用mini-batch(小批量更新)和 full-batch(全批量更新)两种方式。mini-batch在每轮学习(称为1个epoch或1次迭代,即把训练样本全部轮一遍)过程中,分批处理,使用部分样本进行参数更新,直到全部样本训练完成。这种方法的好处是数据量少,资源消耗少,速度快。每轮次的损失函数为所有mini batch的平均损失值。如果每次mini batch中样本个数为m,那么参数的更新方程中的正则化项需修正为:
L1正则化项:\(\displaystyle \frac{\lambda}{m}\sum_w |w|\), L2正则化项:\(\displaystyle \frac{\lambda}{2m}\sum_w w^2\)。full-batch不用修正。
3.3.4 正则化小结
正则化可以降低模型的复杂度,避免模型过分拟合训练数据,包括噪声与异常点(outliers)。另一方面,正则化即是假设模型参数服从一定的先验概率,即为模型参数添加先验(不同的正则化方式为不同的先验分布)。这就规定了参数的分布,使得模型的复杂度降低(简言之,限定条件越多,模型的复杂度越低),这样模型对于噪声与异常点的抗干扰性的能力增强,从而提高模型的泛化能力。
L1正则化与L2正则化的区别在于:L1正则化是拉普拉斯先验,而L2正则化是高斯先验。它们都是服从均值为0,协方差为\(\frac{1}{\lambda}\)。当\(\lambda = 0\)时(即没有先验,没有正则化项),相当于先验分布具有无穷大的协方差,则先验约束非常弱,模型为了拟合所有的训练集数据, 参数\(w\)可以变得任意大从而使得模型不稳定,即方差大而偏差小。\(\lambda\)越大,表明先验分布的协方差越小、偏差越大,模型越稳定。也就是说,正则化项是在偏差bias与方差variance之间做平衡的tradeoff。图1为L1与L2正则化的区别:

图1中的模型是线性回归,有两个特征,要优化的参数分别是\(w_1\)和\(w_2\),左图是L2正则化,右图是L1正则化。蓝色线是优化过程中遇到的等高线,一圈代表一个目标函数值,圆心是某一个样本观测值,半径为误差值。正则化相当于增加了受限条件(红色边界),二者相交处是最优参数。可见L1正则化的最优参数只可能在坐标轴上,从而出现0权重参数,使得模型稀疏。
3.4 Dropout
正则化是通过在代价函数后面加上正则化项来防止模型过拟合,Dropout方法是通过修改人工神经网络(ANN)中隐藏层的神经元个数来防止过拟合。该方法是在对网络进行训练时用一种技巧(trick),对于如下所示的三层人工神经网络:

对于图2的神经网络,在训练开始时,随机删除一些(可以设定为一半,也可以为1/3,1/4等)隐藏层神经元,即认为这些神经元不存在,同时保持输入层与输出层神经元的个数不变,这样便得到如下的ANN:
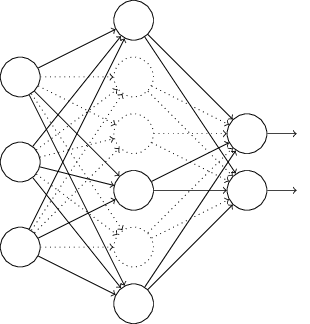
然后按照BP学习算法对ANN中的参数进行学习更新(虚线连接的单元不更新,因为认为这些神经元被临时删除了)。这样一次迭代更新便完成了。下一次迭代中,同样随机删除一些神经元。后续训练过程循环进行这一操作,直至训练结束。
Dropout能够有助于防止过拟合的简单解释,运用了dropout的训练过程,相当于训练了很多个只有部分隐层单元的神经网络(简称“部分网络”)。每一个这样的部分网络,都可以给出一个分类结果,这些结果有的是正确的,有的是错误的。随着训练的进行,大部分半数网络都可以给出正确的分类结果,那么少数的错误分类结果就不会对最终结果造成大的影响。