主成分分析与独立成分分析

发表于 更新于 分类于 ，

　　主成分分析(Principle Component Analysis, PCA)和独立成分分析(Independent Components Analysis, ICA)，是目前应用最为广泛的机器学习数据预处理的手段之一。

　　PCA，顾名思义，取信号中的最为主要的成分，对非重要部分进行去除，从而达到数据降维的目的，避免维度灾难。PCA只对符合高斯分布的样本较为有效。

　　ICA，是盲源分离(Blind source separation, BSS)的一个特例，来源于“鸡尾酒会问题”，如果被观测信号由若干个统计独立的分量的线性组合（混合信号），ICA的目的是将被观测信号解混为若干独立信号源，从而对感兴趣的信号进行处理。

1、PCA

1.1 一个简单的例子

　　二维平面上有若干个样本点，现在希望使用1维坐标对其进行降维处理，同时又希望尽量保留原始的信息，如何实现？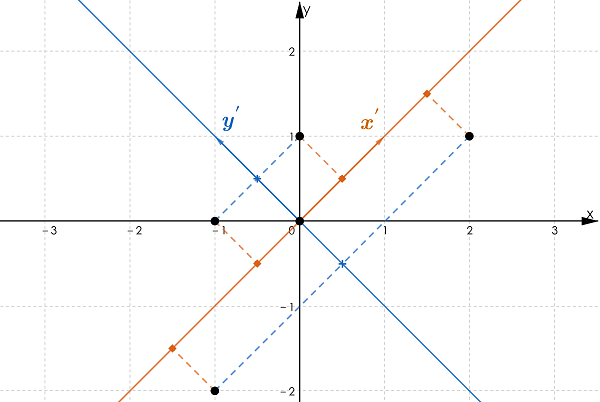

1.2 最大方差理论

　　最懒的一种降维方法，直接将数据点投影至\(x\)/\(y\)坐标轴。这样处理的结果会使得样本叠加，导致有效样本减少，从而丢失信息。例如，所有的样本投影至\(x\)上，此时横坐标上只有3个点，这就造成了原始样本丢失的情况。更为极端的一个例子，如果5个点的横坐标均相同，则投影后只剩下1个点（此时各点在\(x\)轴的方差为0）。如果选择\(y=x\)作为基准坐标轴，可以发现，5个点的信息都会被保留下来。可以看出，方差是衡量样本信息量的关键指标。 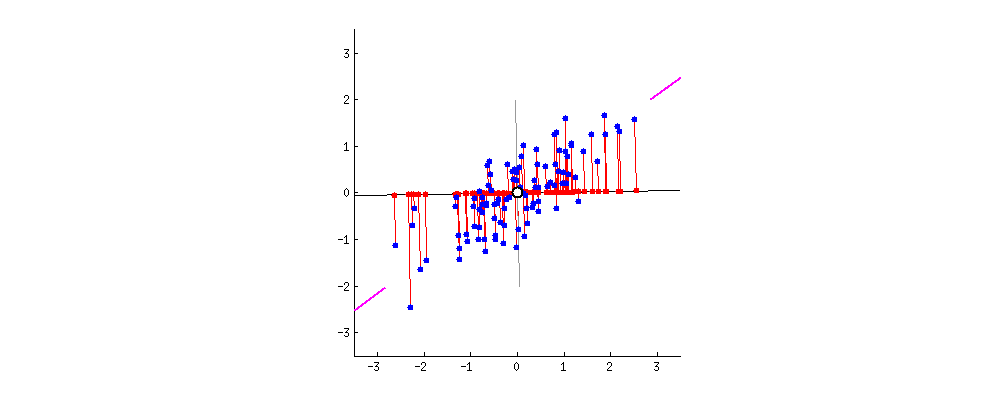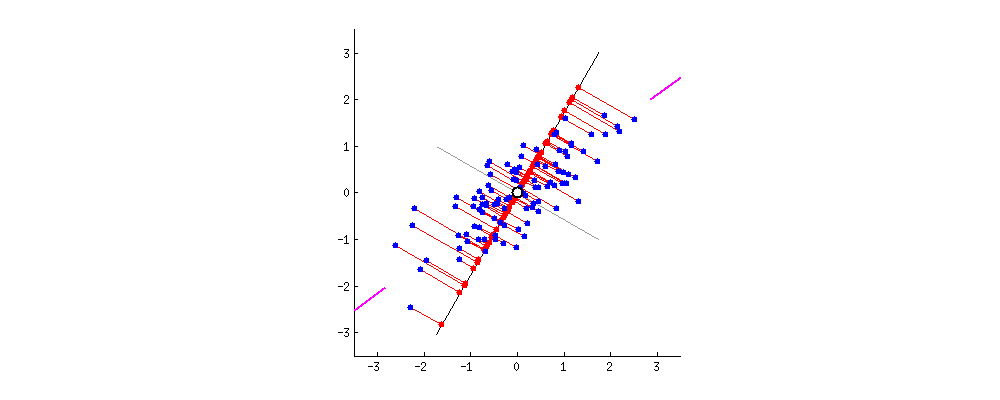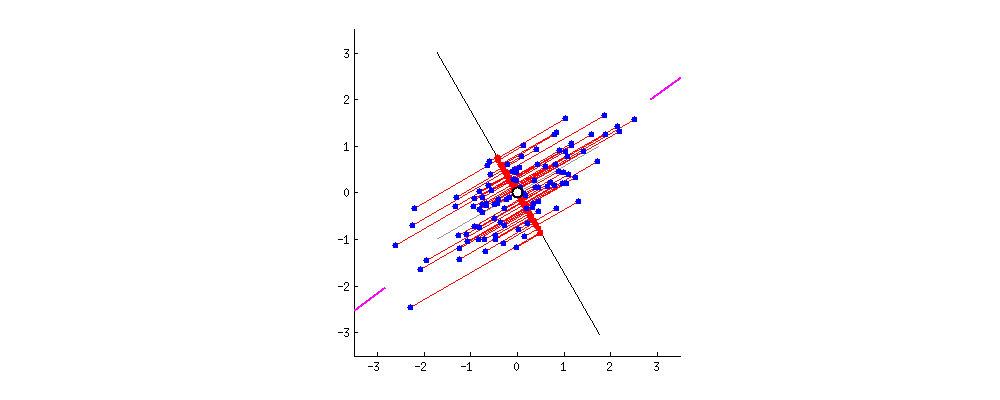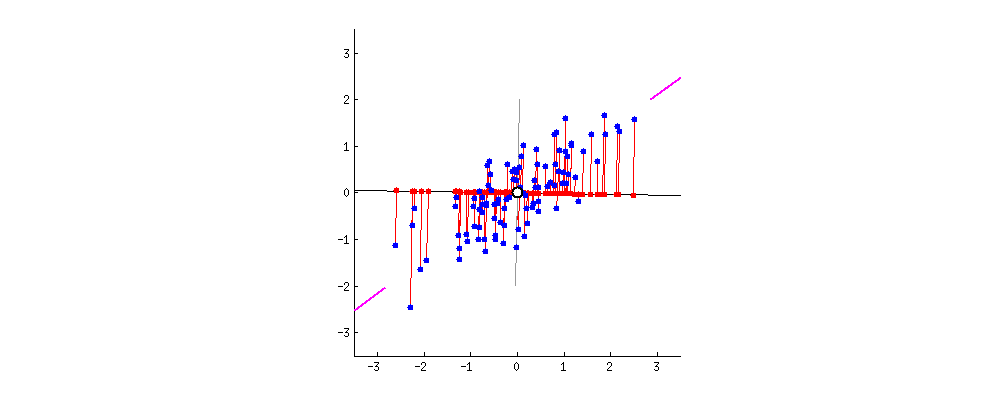　　从信号处理的角度来说，一个随机信号最有用的信息体包含在方差里，方差越大，信号所包含的信息量越多。另一方面，样本的多样性，是保证机器学习算法能够有效学习到特征的前提条件，而方差即为反应样本多样性的关键指标。如图2所示，基向量不同，样本在基向量上的投影长度（方差）不同。设想一组由10个方差为0的数据构成的样本，方差为0说明这10个数据完全相等，故实际有效的样本仅为1个。因此最大化方差，即意味着最大化样本的多样性。图1中，样本在\(x'\)轴上的投影方差较大，在\(y'\)轴上的投影方差较小。当希望将样本数据从二维降至一维时，可以认为选择\(x'\)轴丢失的信息量较少，是较为合理的选择。

　　因此，如果需要对\(n\)维特征数据进行降维处理，如果能够找到\(k (k<n)\)维特征，使得\(\sum_{i=1}^{k} \sigma_{i}^{(k)} \approx \sum_{i=1}^{n} \sigma_{i}^{(n)}\)，那么\((n-k)\)维数据都属于冗余数据，可以丢弃，从而使计算量大大下降。

　　这里有2个问题：

  1. 如何使得所选维度上方差最大？
  2. 在找到第一个维度之后，如何找第二个使得方差最大的维度，且与前一个维度线性无关？

1.3 PCA方法

　　PCA在数学上定义为，一个将原数据变换到新坐标系统下的线性变换，要求原数据投影后，最大方差位于第一坐标轴上（称为第一主成分），第二大方差位于第二坐标轴上（第二主成分），以此类推。

　　以一个随机信号\(\vec{x}=\left [ x_1,\cdots,x_p \right ]\)为例，PCA的基本思想是找到一个向量\(\vec{w}_1\)，使得随机信号在该方向上的投影的方差\(\left (\vec{w}^T_1 \vec{x} \right )\)最大。然后，在与\(\vec{w}_1\)向量正交的空间里到向量\(\vec{w}_2\)，使得信号在\(\vec{w}_2\)投影的方差\(\left (\vec{w}^T_2 \vec{x} \right )\)最大，以此类推直到找到所有向量，用这种方法我们最终可以得到一列非相关的随机变量\(\left [\vec{w}^T_1 \vec{x}, \cdots, \vec{w}^T_n \vec{x} \right]\)。

　　设各特征列均值为\(0\)的样本集\(X\)，由\(n\)个包含\(p\)个特征的样本构成(注意：每行一个样本，每列一个特征)，即：

\[ X=X_{np}= \label{eq1} \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1p} \\ x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{np} \end{bmatrix} \]

　　注1：对一般样本集\(X'\)，可以简单的将各元素减去所在特征列的均值，即可得到特征列均值为0的样本集\(X\)。记\(X'\)各特征列的均值为 \(\bar{X_{p}'} \equiv \left [ \bar {X_{1}'}, \bar {X_{2}'}, \cdots, \bar {X_{p}'} \right ]\) ，则：

\[ X \equiv X' - {\begin{bmatrix} 1& \cdots & 1 \\ \end{bmatrix}}^T_{n} \cdot \bar{X_{p}'} \label{eq2} \]

　　下文讨论均对去均值后的样本集\(X\)展开。

　　对样本矩阵\(X_{n \times p}\)，找到一组由基向量\(\vec{w_i}=[w_1,\cdots,w_p]^T\)构成的矩阵\(W_{p \times p}\)，使得\(Y=X W\)，其中：

  • \(Y\)各分量线性无关；
  • \(Y_1, \cdots,Y_p\)的方差递减；
  • 构成矩阵\(W\)的各基向量\(w_i\)模值为\(1\)，即\(\lVert w_i \rVert=1\)（\(L1\)范数）；

　　考虑方差为协方差矩阵的对角线元素，且当各分量线性无关时，协方差为0，即满足上述条件：

\[ \begin{align*} \label{eq3} Var(Y) &= Cov(Y) = \frac{1}{n-1}Y^T Y \\ &= \frac{1}{n-1} (XW)^T (XW) \\ &= \frac{1}{n-1} W^T X^T X W \\ &= W^T \left( \frac{1}{n-1} X X^T \right ) W \\ &= W^T Cov(X) W \\ \end{align*} \]

　　\(Cov(Y)\)和\(Cov(X)\)以及\(W\)均为对称方阵(\(W^T=W^{-1}\))，从而：

\[ \begin{align*} \label{eq4} Cov(Y) &= W^T Cov(X) W = W^{-1} Cov(X) W \\ &\Rightarrow W Cov(Y) W^{-1} = W W^{-1} Cov(X) W W^{-1}\\ &\Rightarrow W Cov(Y) W^T = Cov(X) \end{align*} \]

　　因此上述问题等价于：求矩阵\(W\)(每列为一个基向量)，使随机信号\(X\)的协方差矩阵的对角化（对称矩阵变为对角矩阵）：

\[ \text{求}w\text{使}：\; \max \limits_{\lVert w \rVert=1} \{Var(W^T X) \} \; \Leftrightarrow \; \text{求} w \text{使}：\{W^T Cov(X) W \} \text{为对角矩阵} \]

　　常规的矩阵对角化方法，有特征值分解(Eigenvalue Decomposition, EVD)，奇异值分解(Singular Value Decomposition, SVD)等。其中EVD针对\(N \times N\)方阵，SVD是EVD的一个推广，可以针对任意形状矩阵。

1.4 矩阵的对角化

　　利用EVD或SVD方法，我们可以将协方差矩阵对角化，并求出相应的变化基向量矩阵。

　　矩阵对角化定理(Matrix diagonalization theorem)：对于\(m\)维方阵\(C\)，如果它有\(m\)个线性无关的特征向量，那么存在一个特征分解：

\[ C = W \Lambda W^{−1} \]

　　其中， \(W\)为\(m \times m\)方阵，且\(W\)的第 \(i\) 列为 \(C\) 的特征向量\(\vec{q_i}\)。\(\Lambda\)是对角矩阵，其对角线上的元素为对应的特征值，即 \(\Lambda_{ii}=\lambda_i\) 。

　　对称对角化定理(Symmetric diagonalization theorem)：更进一步，如果方阵\(C\)是对称方阵，可得\(W\)的每一列都是\(C\)的互相正交且归一化（单位长度）的特征向量，即\(W^{−1}=W^{T}\) 。

　　求出基向量矩阵\(W\)后，特征值矩阵 $ $ 已经按照各特征值(方差)大小排列，故可以根据重要性，简单的选取前\(k\)个向量即可。设需要取 \(k (1 < k < m)\) 个基向量（例如前\(k\)个特征值占全部\(p\)个特征值的\(90\%\)，即\(\sum^k_{i=1} \lambda_i / \sum^p_{i=1} \lambda_i > 0.9\)），令\(W_{p \times k}\)为\(W\)的前\(k\)维基向量子矩阵，则变换后的数据\(Y\)为：

\[ Y = X W_{p \times k} \]

　　其中，新的数据矩阵\(Y\)为\(n \times k\)矩阵，较原\((n \times p)\)维数据矩阵\(X\)，减少了\((p-k)\)维，从而达到了降维的目的。

1.5 奇异值分解

　　奇异值分解定义：假设\(X\)是一个\(n×p\)阶矩阵，其中的元素全部属于域\(K\)(实数域或复数域)。如此则存在一个分解使得

\[ M=U \Sigma V^* = U \Sigma V^{T} \quad (V\text{为实矩阵}) \]

　　其中\(U\)是\(n×n\)阶酉矩阵(也叫幺正矩阵)；$ \(是\) m n \(阶非负实数对角矩阵；\)V$的共轭转置 $ V^{*} \(，是\)p p\(阶酉矩阵（当\)V\(为实矩阵时，\)V^*=V^T\(）。这样的分解就称作\)M\(的奇异值分解。\)\(对角线上的元素\)_{i,i}\(即为\)M$的奇异值。如图3所示：

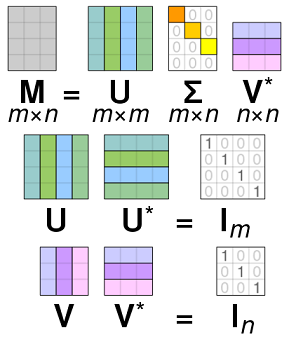
　　设\(Cov(X)=WLW^{T}\)，考虑矩阵\(X\)的奇异值分解：\(X=U\Sigma V^T\)，且\(\Sigma 为实对角矩阵\)，则：

\[ \begin{align*} \left \{ \begin{array}{r@{\mskip\thickmuskip}l} Cov(X) &=& \underline{WLW^{T} } \\ Cov(X) &=& \displaystyle \frac{1}{n-1} X^{T} X \\ X\ &=&\ U \Sigma V^{T} \\ \end{array} \right . \, \implies \, \begin{array}{r@{\mskip\thickmuskip}l}\\ Cov(x) &=& \displaystyle \frac{1}{n-1} \left ( U\Sigma V^{T} \right )^T U\Sigma V^{T} \\ &=& \displaystyle V \frac{\Sigma^T \Sigma}{n-1} V^T = \underline{\displaystyle V \frac{\Sigma^2}{n-1} V^T} \end{array} \end{align*} \]

　　比较式中划线部分的协方差\(Cov(X)\)的表达式，可以发现：

\[ \begin{array}{r@{\mskip\thickmuskip}l} WLW^{T} =\displaystyle V \frac{\Sigma^2}{n-1} V^T \\ \end{array} \; \implies \; \left \{ \begin{array}{r@{\mskip\thickmuskip}l} W &=& V &\, & \text{(基向量 vs 右奇异矢量)} \\ L &=& \displaystyle \frac{1}{n-1}\Sigma^2 &\, & \text{(特征值 vs 奇异值)} \\ \end{array} \right. \]

　　上式说明，奇异值分解后的右奇异矢量与特征向量是一样的，即主成分方向向量；特征值矩阵\(L\)和奇异值矩阵\(\Sigma\)之间的关系为\(\lambda_{i} = \Sigma^2_{ii}/(n-1)\)。主成分由\(XV = USV^T V= US\)给出。

1.6 PCA的计算

　　特征值分解和奇异值分解均能实现PCA功能，以下代码使用SVD方法进行： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
import numpy as np
from sklearn import decomposition

def pca(data,threshs=0.9):
    '''
        实现pca降维，行向量为样本数，列向量为特征数
    '''
    # 去均值
    data = data - data.mean(axis=0)
    
    # SVD分解
    _,s,vh = np.linalg.svd(data)

    # 由奇异值求特征值
    s = s*s/(data.shape[0]-1)

    # 计算特征值累积占比
    # print('特征值累积占比:')
    cum =np.cumsum(s)/s.sum()
    #print(cum)

    # 寻找距离阈值最小的索引
    k = np.argmin(np.abs(cum-threshs))

    k = k + 1

    return data.dot(vh.T[:,:k])


def sk_pca(data,ncoms=1):
    '''
    使用sklearn函数求解pca
    '''
    data = data-data.mean(axis=0)
    dec = decomposition.PCA(n_components=ncoms)
    dec.fit(data)
    # print(dec.singular_values_)
    return dec.fit_transform(data)


n=10
p=5

d = np.random.randn(n,p)
for i in range(2,p):
    d[:,i] = d[:,i-2]*0.2 + d[:,i-1]*0.1 + d[:,i]*3
d
# Out[38]: 
# array([[ 0.3339,  0.289 , -0.1083,  0.8498, -6.5554],
#        [-0.1016, -0.7047,  0.4679,  4.3804,  1.1741],
#        [ 0.3309, -0.1823, -3.3715,  2.7843,  2.1753],
#        [-0.5411,  0.3759, -1.3554,  3.3289, -4.585 ],
#        [-1.8377, -1.2617,  7.2369,  4.0068, -0.5727],
#        [ 0.1038, -0.958 , -3.85  , -3.3861, -0.3578],
#        [ 2.4289, -0.6595, -0.8572, -4.1682, -1.2252],
#        [ 0.228 ,  0.6531,  3.0009,  4.116 ,  0.2939],
#        [ 1.7679, -1.2958,  2.9587,  1.7904, -0.1354],
#        [-0.9489, -0.2181, -1.1429, -0.4187, -1.6981]])

p1 = pca(d)
p1
# Out[39]: 
# array([[-1.3118, -5.1628, -1.2068],
#        [ 2.4578,  2.5278, -1.5113],
#        [-1.3398,  4.2623, -2.5864],
#        [-0.2347, -2.7441, -3.4702],
#        [ 7.1897, -0.958 ,  2.3557],
#        [-6.0142,  1.3158,  0.9834],
#        [-4.7649, -0.2436,  3.5921],
#        [ 3.9656,  0.9283, -0.1481],
#        [ 2.1713,  0.5124,  2.04  ],
#        [-2.1189, -0.4381, -0.0484]])

sk_pca(d,p1.shape[-1])
Out[40]: 
# array([[-1.3118,  5.1628, -1.2068],
#        [ 2.4578, -2.5278, -1.5113],
#        [-1.3398, -4.2623, -2.5864],
#        [-0.2347,  2.7441, -3.4702],
#        [ 7.1897,  0.958 ,  2.3557],
#        [-6.0142, -1.3158,  0.9834],
#        [-4.7649,  0.2436,  3.5921],
#        [ 3.9656, -0.9283, -0.1481],
#        [ 2.1713, -0.5124,  2.04  ],
#        [-2.1189,  0.4381, -0.0484]])

# 两者比较，中间维度数值正确，符号相反，
# 这是np.linalg.svd计算和np.linalg.eig计算结果差异造成的

np.allclose(np.abs(p1), np.abs(p2) )
# Out[41]: True


　　上述代码使用了SVD计算特征向量和特征值，numpy中的svd函数计算结果中，特征向量已经按照特征值的降序排序。numpy文档中有如下说明：

numpy.linalg.svd(a, full_matrices=True, compute_uv=True, hermitian=False)
Returns
  s : (…, K) array
    Vector(s) with the singular values, within each vector sorted in descending order.

numpy.linalg.eig(a)
  Returns:    
    w : (…, M) array
    ... The eigenvalues are not necessarily ordered. ...

　　在小样本时，自己编写的函数速度较快，但是对于大样本，还实用sklearn的函数吧。另一方面，对于大样本，sklearn还有一个IncrementalPCA函数，可以实现批PCA。同样，函数以计算的精确度为代价，换区少量内存的使用。

2、ICA

　　待续

参考